Recently, while implementing EfficientNet networks I came across a github comment detailing an implementation of Swish activation function that promises saving upto 30% GPU memory usage for EfficientNets. In this (short) blog post I will briefly go over the details of this implementation and explain what enables this implementation to save GPU memory.

More precisely in this post I will cover:

• What is a Swish activation function?
• How is Swish implemented?
• Why simple Swish implementation is inefficient?
• How is the memory efficient version Swish implemented?
• What makes this implementation save GPU memory?
• How much GPU memory is saved?

The content of this post is largely based on the original github comment. To benchmark the memory usage, I use EfficientNet implementation from MONAI. All codes discussed below are written using current PyTorch release and hence I assume the reader has basic knowledge of how simple modules can be written in PyTorch.

I have written the following script to report memory usage in this post:

https://github.com/masadcv/MONAIMemoryEfficientSwish

What is a Swish activation function?

First proposed in paper from Google Brain team, Swish is an activation function that has recently been used in deep learning models, including MobileNetV3 and EfficientNets. Mathematically, Swish function is defined as:

where \(\text{Sigmoid}(x) = \frac{1}{1+e^{-x}}\) is the Sigmoid acitvation function. This Swish activation function has the following graph:

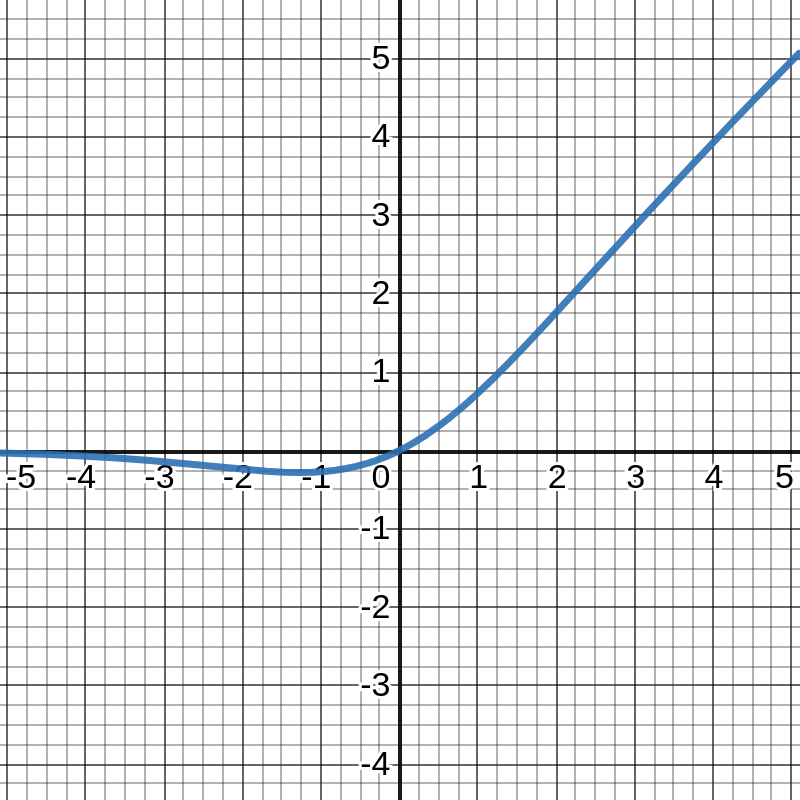
In the original paper and both MobileNetV3 as well as EfficientNets, Swish has been shown to enable models that surpass the existing state-of-the-art for ImageNet classification task.

How is Swish implemented?

Implementing Swish is quite straightforward as we only need to implement the equation \(\text{Swish}(x) = x ~ \text{Sigmoid}(x)\). This can be done as a simple PyTorch module as follows:

class Swish(nn.Module):
    def __init__(self, alpha=1.0):
        super().__init__()
        self.alpha = alpha

    def forward(self, input: torch.Tensor) -> torch.Tensor:
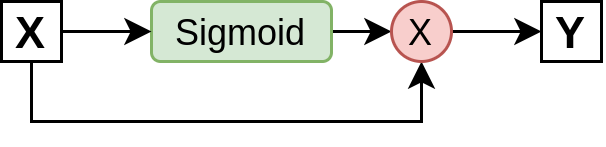
        return input * torch.sigmoid(self.alpha * input)

This module forms the following graph, which shows application of Swish activation to an input X to form the corresponding output Y. The black arrows indicate a forward pass for our function.

Why simple Swish implementation is inefficient?

The straightforward Swish implementation shown above takes significantly more memory as compared to other existing activation functions (e.g. ReLU, Sigmoid, Tanh). The reason for this can be understood with reference to the following graph, which shows forward (black arrows) and backward (red arrows) passes for this module.

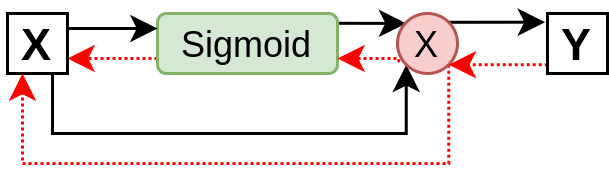
The backward pass propagates gradients corresponding to three featuremaps. These are 1) input featuremap (\(x\)), 2) \(\text{Sigmoid}(x)\) output featuremap and 3) Swish output featuremap (\(x ~\text{Sigmoid}(x)\)). Next we look at how a memory efficient version of Swish can be implemented and what enables it to save upto 30% GPU memory.

How is the memory efficient version Swish implemented?

The main memory overhead in our simple Swish implementation comes from having multiple featuremaps, which need to be preserved in memory in order to do the backward pass. To improve the memory efficiency, we would need to reduce this - which is exactly what is achieved with the implementation from the original github comment. It implements Swish as a single module, where gradient for only the input (\(x\)) is calculated. This hides the intermediate gradients and hence only requires saving input (\(x\)) - resulting in significantly reduced memory requirements.

Let’s look at the memory efficient Swish code:

class SwishImplementation(torch.autograd.Function):
    @staticmethod
    def forward(ctx, input):
        result = input * torch.sigmoid(input)
        ctx.save_for_backward(input)
        return result

    @staticmethod
    def backward(ctx, grad_output):
        input = ctx.saved_tensors[0]
        sigmoid_input = torch.sigmoid(input)
        return grad_output * (sigmoid_input * (1 + input * (1 - sigmoid_input)))

class MemoryEfficientSwish(nn.Module):
    def forward(self, input: torch.Tensor):
        return SwishImplementation.apply(input)

And the updated memory efficient Swish module:

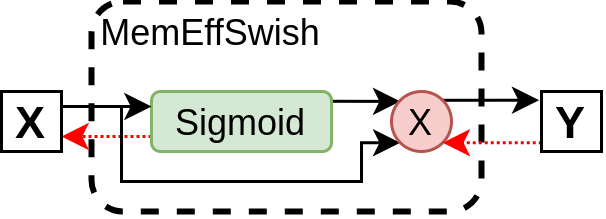
What makes this implementation save GPU memory?

The trick that enables this alternate implementation work, is that only the input featuremap is saved and used for gradient calculation. A minor overhead this has is increasing the computation for backward pass. In order to understand how this can be done, let’s work out the gradient of Swish:

Recall that Swish is defined as:

In order to do backpropagation, we need to work out partial derivative of \(\text{Swish}\) w.r.t \(x\), i.e. \(\frac{\partial ~ \text{Swish}}{\partial x}\). This can be achieved with product rule as:

where \(U = x\) and \(V = \frac{1}{1+e^{-x}}\).

We can start substituting and simplifying:

It would be helpful now to have the term \(\frac{e^{-x}}{(1+e^{-x})}\) represented in terms of \(\text{Sigmoid}\) (i.e. \(\frac{1}{(1+e^{-x})}\)). This can be easily achieved with a simple trick. We first add and subtract \(\pm 1\) from the numerator:

Now separate the \(-1\):

Simplifying we get:

We now have everything we need to get to a single gradient equation that only requires input \(x\). Let’s substitute everything back and simplify the original partial derivative equation:

Lastly, we can replace \(\text{Sigmoid}(x) = \frac{1}{1+e^{-x}}\) to get our simplified differential equation:

Notice this equation only depends on input \(x\) and hence in our forward pass we only need to preserve \(x\).

How much GPU memory is saved?

Finally, let’s look at how much improvement in memory allocation we can have with this simple trick.

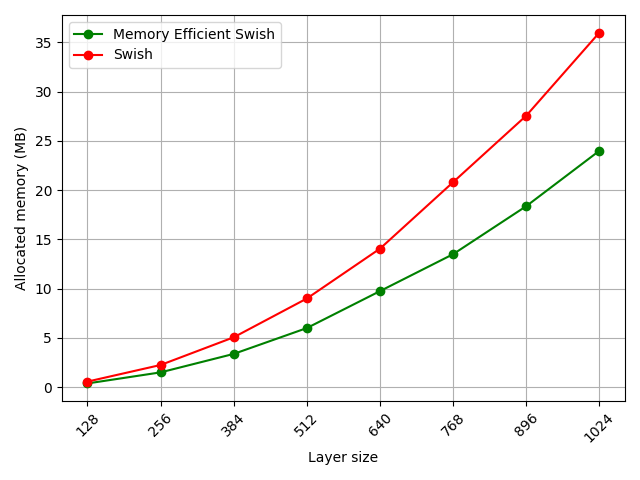
For different EfficientNet models we see a significant improvement in memory requirements:

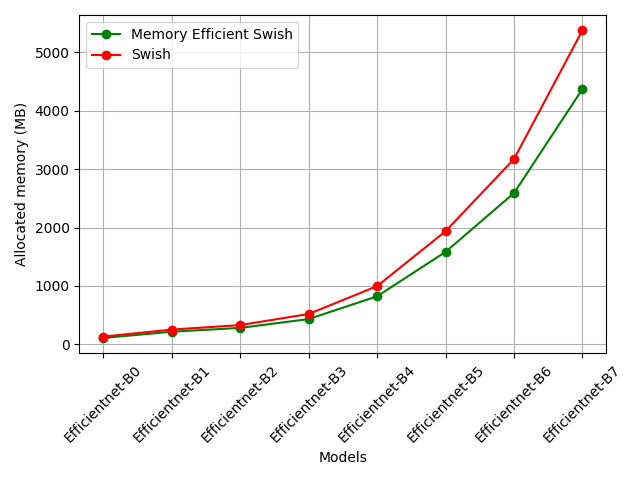
The improvement is significant, especially for bigger EfficientNet models. This is due to the fact that bigger models have both bigger as well as more featuremaps.

Lastly, we can also see improvements w.r.t the size of a single featuremap. This again shows significiant improvement, even greater than in EfficientNets, which roughly corresponds to the original ~30% improvement reported in the original github comment.